关于八字倒角的信息

前面已经分享了四边形综合、圆综合的解题思路。

接下来总结下其他综合的题的解题思路，供孩子们高效准备好中考。

本文介绍：尺规作图、一元二次方程综合题、一次反比例函数综合题、代数综合题、几何综合题、新定义题目的解题思路和知识点。

尺规作图题

注意点

会尺规作图垂直平分线知道垂直平分线的性质定理和判定定理知道中位线定理知道圆周角定理和推论会尺规作图角平分线会做三角形的外接圆和内切圆一元二次方程综合题

注意点

会找a，b，c,不要忘了带符号。知道a≠0知道判别式△的公式知道当△＞0、△≥0、△＝0、△＜0四种情况根的情况知道通过配成完全平方的形式判定△和0的大小关系题目若告知某个根的具体值，则把根代入求出参数，再计算知道一元二次方程求根公式，会用公式求根。也可用十字相乘法。若告知某个根的范围，求参数值。则用公式法或因式分解法把根求出来，再算范围（第一）题目若描述为一元二次方程或方程有两个根，则必须保证a≠0；（第二）题目若没有明确描述方程为一元二次方程，则需要分a＝0和a≠0分类讨论。一次反比例函数综合

1、题型有哪些？

第一问：求反比例函数解析式，一次函数解析式和参数，求坐标；简单题，细心做，不丢分。

第二问：整点问题、线段长度关系问题、面积问题、图像交点问题。

2、第二问解法

（1）如果第二问分两小问，那么第1小问比较简单，需要准确画出函数图像即可，此问不丢分。

（2）第二问的第2小问，相对较难。处理办法如下

整点问题

方法：①明确函数图像随参数的变化趋势（直线包括过定点的直线和平行直线，双曲线包括固定双曲线和

沿着y=x,y=-x变化的双曲线）；②分类讨论，分类范围一是上小问为起点的上下范围；二是特殊值的上下范围，

特殊值包括1，-1等情况。

线段长度关系问题

方法：①明确函数图像随参数的变化趋势（直线包括过定点的直线和平行直线，双曲线包括固定双曲线和

沿着y=x,y=-x变化的双曲线）；②向坐标轴作垂线，将线段长度问题通过相似三角形转化成坐标问题。

③分类讨论，分类范围一是上小问为起点的上下范围；二是特殊值的上下范围，

特殊值包括1，-1等情况。

面积问题

方法：①向坐标轴作垂线，将面积拆分，注意试验向两个坐标轴作垂线，不是每个垂线都能解决问题。②

有些题可以写出面积的解析式，再根据解析式求面积。

图相交点问题

方法：①明确函数图像随参数的变化趋势（直线包括过定点的直线和平行直线，双曲线包括固定双曲线和

沿着y=x,y=-x变化的双曲线）；②分类讨论，分类范围一是上小问为起点的上下范围；二是特殊值的上下范围，

特殊值包括1，-1等情况。

代数综合

第一问：

求坐标，比较简单，代入即可；

求对称轴，三种方法，对称性、公式法、配成顶点式；

注意：有时候会通过二次函数与x轴的交点距离求对称轴或解析式，熟悉二次函数与一元二次方程的转化。

第二问：

（1）对称性、求区间最值问题

注意根据区间和对称轴的位置关系，分类讨论。

巧用列不等式求解关系。

（2）与线段交点问题，整点问题、创新题。

方法：

（1）判断抛物线的运动变化趋势，这个很重要很重要 很重要

形状是否定，

对称轴是否定，

是否过定点，

顶点是否固定

（2）分类讨论

类范围一是上小问为起点的上下范围；二是特殊值的上下范围，

特殊值包括1，-1等情况。

（3）常见方法

运动法

*

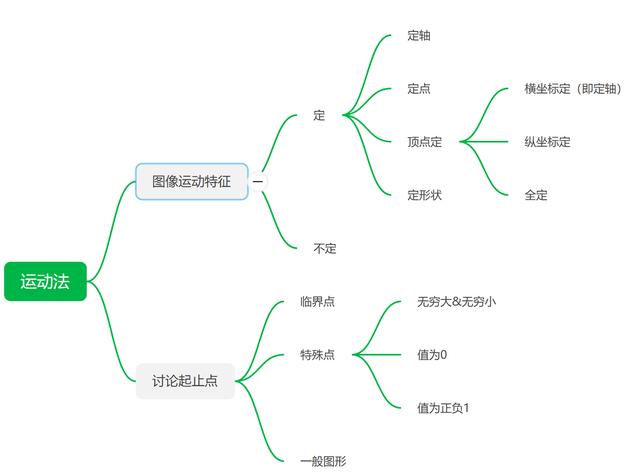
几何综合

常见题型

问题1：补全图形

答题要点

（1）注意易看错：旋转中心和旋转方向。

（2）注意易忽略：是射线旋转还是线段旋转。

（3）画图务必标准，才能对后面的角度和线段关系计算提供测量依据。

问题2：求角度

考情：

（1）一个角，求角度。

通常是特殊角度或α加减特殊角度。

优先用量角器测量。

也可取特殊位置，猜想出角度，再推广到一般情况。

（2）两个角，求角度关系，通常是等量关系或者2倍，3倍等倍数关系，或者互补互余关系。

同样优先量角器方法和特殊位置方法。再根据结果寻找论证思路。

倒角思路和方法：

（1）角度倒角

寻找等角，等量代换；

构造目标角度，论证目标；

（2）位置倒角

构造或寻找平行线，三线八角倒角

构造或寻找垂线，通过同角的余角关系倒角

寻找对顶角，通过对顶角倒角

寻找共线，通过邻补角倒角

寻找轴对称，通过对称倒角

（3）图形倒角

三角形倒角（四种方法）：内角和，外角，等边对等角，全等相似。

四边形倒角（2种方法）：四边形对角互补，平行四边形。

圆倒角（3种方法）：四点共圆，同弧圆周角，圆内接四边形性质。

（4）代数倒角

设未知数，通过方程思想倒角。

取特殊位置或特殊值，若满足一般情况，则一定满足特殊情况。

作差 作和

（5）模型倒角

八字倒角模型

（6）量角器量角

问题3：求线段关系

考情

（1）一条线段，求线段长度

通常是特殊值，或满足特殊关系。

（2）两条线段，求线段关系

通常是相等关系或者整数倍关系，根号2，根号3倍关系。

（3）三条线段，求线段关系

情况一：三条线段满足和的关系，或者整数倍和的关系，或者根号2、根号3倍和差关系。

情况二：三条线段满足勾股关系，或者倍数勾股关系，或者根号2、根号3倍勾股关系。

解题思路

思路一：考虑几何综合模型

包括：手拉手模型，空翻模型，中点角分线模型，半角模型，弦图（一线三等角），轴对称。

思路二：考虑寻找或构造全等三角形

思路线索

在和几何模型不相关的几何线段证明中。寻找和构造全等三角形是根本思路。本质上几何综合模型也是在构造全等三角形。

寻找构造方法

第一步：重点关注（1）题目中的等角度或等线段（2）上一问证明的等角度或等线段（3）目标的等线段或等角度

第二步：寻找包含这些元素的三角形，确定全等三角形。

第三步：确定全等条件，证明全等。

思路三：寻找特殊情况，有特殊情况确定目标，再论证。

思路四：优先用尺子测量。

问题4：最值问题

考情

（1）问线段的最值，或三角形面积的最值

通常是寻找点的轨迹。

常见轨迹是：圆或直线。

（2）问两条线段和的最值。

通常是利用将军饮马模型。

（3）三角形两边之和大于第三边

通常选择填空题会用三角形三边关系。在几何综合题目更多题目是用找轨迹

新定义压轴题

解题思路

1、第一问送分题 ，不要丢分

2、第二三问解题思路

三个思考方向：找轨迹、找临界、运用几何方法计算

（1）找轨迹

轨迹通常是圆相关的图形，需要注意 。

（2）找临界

不必考虑是否充分正确，临界一般是相切和情况和过端点的情况，代入即可。

（3）计算

通常是向坐标轴作垂线，通过勾股、相似、特殊角度、方程等方法计算。