八字神数(个人命盘详解免费版)

八位走马灯神数

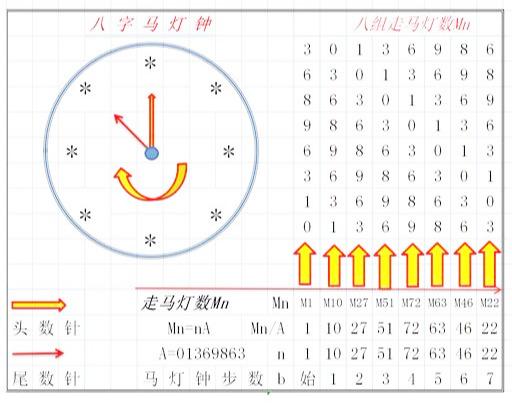
一、八位走马灯神数01369863

（一）神数01369863的重新排列

把01369863的1，10，27，51，72，63，46，22倍做成开头数字为0，1，3，6，9，8，6，3的8组神数：

01369863=1*01369863

13698630=10*01369863

36986301=27*01369863

69863013=51*01369863

98630136=72*01369863

86301369=63*01369863

63013698= 46*01369863

30136986=22* 01369863

这8组数字正好是01369863的重新有序排列；具有走马灯数的特征，可做成“8数字马灯图”

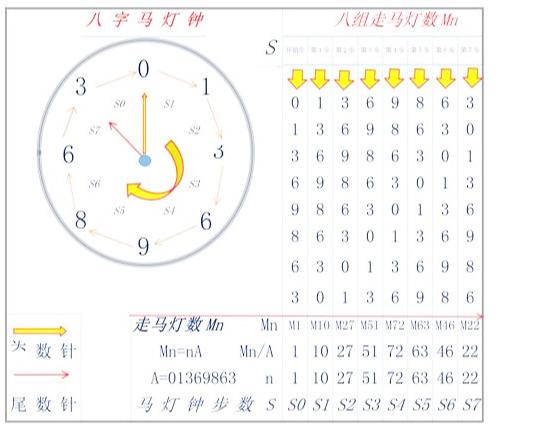
走马灯神数01369863的马灯图

（二） 神数01369863马灯图说明：

①　图右边是开头数字为0，1，3，6，9，8，6，3的8组走马灯数Mn

Mn = n A

A=01369863

n=1，10，27，51，72，63，46，22

M1=1A=1*01369863=01369863

M10=10A=10*01369863=13698630

M27=27A=27*01369863=36986301

M51=51A=51*01369863=69863013

M72=72A=72*01369863=98630136

M63=63A=63*01369863=86301369

M46=46A=46*01369863=63013698

M22=22A=22*01369863=30136986

②　走马灯数是从上到下竖立排列；从M1开始从左到右按照步数S走动：

S0/M1→S1/M10→S2/M27→S3/M51→S4M72→S5/M63→S6/M46→S7/ M22... ...

走马灯数从左到右按列读取：

01369863→13698630→36986301→69863013

→98630136→86301369→63013698→30136986...

n=1→10→27→51→72→63→46→22...

③　图左边是“八字马灯钟”

马灯钟有两根针：头数针和尾数针；

马灯钟的两根针按照顺时针方向同时走动，每步走一个字；

头数针的走字顺序：0→1→3→6→9→8→6→3从头开始...

尾数针的走字顺序：3→0→1→3→6→9→8→6 从头开始...

头/尾数针的每一步对应右图的一组走马灯数；

始步M1/ 01369863→ 1步M10/ 13698630→2步M27/36986301

3步M51/69863013→4步M72/98630136→5步M63/86301369

6步M46/63013698→7步M22/30136986→从头开始...

二、八位走马灯神数00729927

（一）神数00729927的重新排列

把00729927的1，10，100，41，136，127，37，96倍做成开头数字为0，0，7，2，9，9，2，7的8组神数：

07299270=1*00729927

72992700=10*00729927

29927007=100*00729927

99270072=41*00729927

92700729=136*00729927

27007299=127*00729927

70072992= 37*00729927

70072992=96* 00729927

这8组数字正好是00729927的重新有序排列；具有走马灯数的特征，可做成“8数字马灯图”

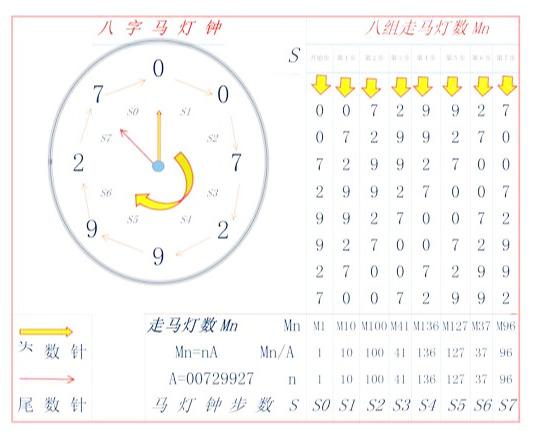
走马灯神数00729927的八字马灯钟

（二） 神数00729927马灯图说明：

①　图右边是开头数字为0，0，7，2，9，9，2，7的8组走马灯数Mn

Mn = n A

A=00729927

n=1，10，100，41，136，127，37，96

M1=1A=1*00729927=00729927

M10=10A=10*00729927=07299270

M100=100A=100*00729927=72992700

M41=41A=41*00729927=29927007

M136=136A=136*00729927=99270072

M127=127A=127*00729927=92700729

M37=37A=37*00729927=27007299

M96=96A=96*00729927=70072992

②　走马灯数是从上到下竖立排列；从M1开始从左到右按照步数S走动：

S0/M1→S1/M10→S2/M100→S3/M41→S4/M136→S5/M127→S6/M37→S7/ M96...

走马灯数从左到右按列读取：

00729927→07299270→72992700→29927007

→99270072→92700729→27007299→70072992...

n=1→10→100→41→136→127→37→96...

③　图左边是“八字马灯钟”

马灯钟有两根针：头数针和尾数针；

马灯钟的两根针按照顺时针方向同时走动，每步走一个字；

头数针的走字顺序：0→0→7→2→9→9→2→7从头开始...

尾数针的走字顺序：7→0→0→7→2→9→9→2 从头开始...

头/尾数针的每一步对应右图的一组走马灯数；

始步M1/00729927→1步M10/ 07299270→2步M100/72992700→3步M41/29927007

→4步M136/99270072→5步M127/92700729→6步M37/27007299→7步M96/70072992

始步M1/ 00729927→ 1步M10/ 07299270→2步M27/72992700

三、八九家族神数

（一）99999999的因子分解

99999999 = 3*3*11*73*101*137；

这6个因子中，任何一个因子或者它与其它因子的乘积都可以成为一个八九神数的根。这个根的倒数是一个无限循环小数。取小数点后面八位数的循环节就是我们要寻找的八九神数。把根除外的剩余因子的乘积，或用这个根去除99999999就可以得到要寻找的八九神数。

走马灯数01369863和00729927的根分别为73,137；根和神数相乘分别为73*01369863=137*00729927=99999999；

把根和神数乘积=99999999的神数称为八九神数。

（二）八九家族神数的素数根和合数根

素数根只有5个：3, 11, 73,101 ,137。

合数根有：9，33，99，219，303，411，657,10001， ... ...

（三）杂交神数和原神数

合数根是2个以上素数的乘积；这些合数根被称为为杂交根，因为它是由两个以上素数杂交（相乘）而成；

和素数根对应的神数被称为父神数，和另外一个素数根对应的神数被称为母神数；和杂交根对应的神数被称为杂交神数，或者子神数；

和父/母神数对应的根被称为父/母根，和子（杂交）神数对应的根被称为子（杂交）根。

（四）走马灯数的杂交神数

父神数,01369863 ，母神数00729927，父根= 73，母根 =137；

杂交根是 73*137=10001。

1/10001=0.0000999900009999...（无限循环小数）

取小数点后面八位数（第一循环节）00009999，这就是我们要找的两个八九走马灯神数

01369863和00729927的杂交（子）神数。

子（杂交）神数=00009999

四、走马灯数的神奇规律

（一）父母神数、父母根与子神数的关系

1. （父神数+母神数）÷ 子神数 = 父根+母根

（01369863+00729927）÷ 00009999=210=73+137

2. （父神数-母神数）÷ 子神数 = 母根-父根

（01369863-00729927）÷ 00009999=64=137-73

3. （父神数平方 + 母神数平方）÷ 子神数平方

= 父根平方 + 母根平方

（01369863平方+00729927平方）÷ 00009999平方

=137平方+73平方=18769+5329=24098

4. （父神数平方 - 母神数平方）÷ 子神数平方

= 母根平方 - 父根平方

（01369863平方-00729927平方）÷ 00009999平方

=137平方-73平方=18769-5329=13440

（二）八九[99999999]规律

1. 父神数×母神数÷杂交神数=99999999

01369863×00729927÷00009999=99999999

2. M前八位 + M后八位 = 99999999

M = 99999999平方 =9999999800000001

99999998+00000001=99999999

3. W的前面八位数+中间八位数的和=99999999

W=99999999立方=999999970000000299999999

99999997+00000002=99999999

4. W的后面8位数=99999999

5. 走马灯数和根的乘积是99999999

01369863*73=99999999

00729927*137=99999999

6. 走马灯数头周期头尾两个数之和以及中间两个数之和都是99999999

①　头尾两个数之和=99999999

走马灯数01369863

头数1*01369863

尾数72*01369863

头数+尾数=（1+72）013698632=99999999

走马灯数00729927

头数1*00729927

尾数136*00729927

头数+尾数=（1+136）00729927=99999999

②　中间两项两个数之和=99999999

走马灯数01369863 中间两项：72/2=36, 36+1=37

中间两个数之和

36*01369863+37*01369863

=（36+37）*01369863=99999999

走马灯数00729927 中间两项：136/2=66, 66+1=67

中间两个数之和

86*00729927+87*00729927

=（66+67）*01369863=99999999

（三）七九[9999999]规律

1．M的前面7位数是9999999

M=99999999平方=9999999800000001

2．W的前面7位数是9999999

W=99999999立方=9999999700000299999999

（四）四九[9999]规律：

1. 两个走马灯数之和÷两个根之和=9999

（1369863+00729927）÷（73+137）

=2099790÷210=9999

2. 两个走马灯数之差÷两个根之差=9999

（1369863-00729927）÷（137-73）

=6399936÷64=9999

3. 走马灯数 ÷（马灯数头四位数+1）= 9999

①　走马灯数01369863

a. 头周期各项

m=01369863n n=1,2,3...73

第1项1*01369863 ： （马灯数头四位数+1）=0137

01369863*0137=9999

第2项2*01369863： （马灯数头四位数+1）=0274

01369863*0274=9999

第3项3*01369863： （马灯数头四位数+1）=0411

01369863*0411=9999

... ... ...

第72项72*01369863： （马灯数头四位数+1）=9864

01369863*9864=9999

b. 它的倒顺序数：

第1项36896310/3690=9999

第2项62793720/6280=9999

第3项98590140/9860=9999

... ... ...

第72项63103689/6311=9999

②　走马灯数00729927

c. 头周期各项

m=00729927n n=1,2,3...173

第1项1*00729927/73=9999

第2项2*00729927/146=9999

第3项3*00729927/219=9999

... ... ...

第72项72*00729927/5256=9999

4. 走马灯数平方是9999的倍数

01369863平方÷187671231 =9999

00729927平方÷53284671 =9999

5. 走马灯数前面4位数+后面4位数之和是9999

走马灯数 01369863 0136+9863=9999

走马灯数 00729927 0072+9927=9999

（五）二九[99]规律：

1. 走马灯数头周期各项和它的倒顺序数都是99的倍数

①　走马灯数01369863

a. 头周期神数各项

m=01369863n, n=1,2,3, ...73

第1项1*01369863/99=13837

第2项2*01369863/99=27674

第n项/99=13837n

第73项99999999/99=1010101

b. 它的倒顺序数

第1项36896310/99=7659

第2项62793720/99=834280

... ... ...

第73项99999999/99=1010101

②　走马灯数00729927

a. 头周期神数各项

m00729927n n=1,2,3, ...137

第1项1*00729927/99=7373

第2项2*00729927/99=14746

... ... ...

第n项/99=7373n

第137项99999999/99=1010101

b. 它的倒顺序数

第1项72992700/99=737300

第2项145985400/99=1474600

... ... ...

第137项99999999/99=1010101

2. 头4位数+尾4位数之和的前后两位数都是 99

走马灯数 01369863 0136+9863=9999

走马灯数 00729927 0072+9927=9999

（六）一九 [9] 规律：

1．走马灯数头周期各项和它的倒顺序数都是都是9的倍数。

①　走马灯数01369863

c. 头周期神数各项

m=01369863n, n=1,2,3, ...73

第1项1*01369863/9=13837*11

第2项2*01369863/9=27674*11

第n项/9=11*13837n

第73项99999999/9=11111111

d. 它的倒顺序数

第1项36896310/9=7659*11

第2项62793720/99=834280*11

... ... ...

第73项99999999/9=11111111

②　走马灯数00729927

c. 头周期神数各项

m00729927n n=1,2,3, ...137

第1项1*00729927/9=7373*11

第2项2*00729927/9=14746*11

... ... ...

第n项/9=11*7373n

第137项99999999/99=1010101

d. 它的倒顺序数

第1项72992700/9=737300*11

第2项145985400/9=1474600*11

... ... ...

第137项99999999/9=11111111

2．各位数字之和也是9的倍数

0+1+3+6+9+8+6+3=27=3*9

0+0+7+2+9+9+2+7=34=4*9